3. Dynamiikka
Dynamiikasta tärkeimpiä asioita ovat Newtonin ensimmäinen- ja toinen laki ja siihen liittyvä voimien tasapaino, liikemäärä, impulssi ja momentti. Tehtävissä saa käyttää valitsemaasi kaavakokoelmaa (esim. MAOL) ja trigonometrista taulukkoa.
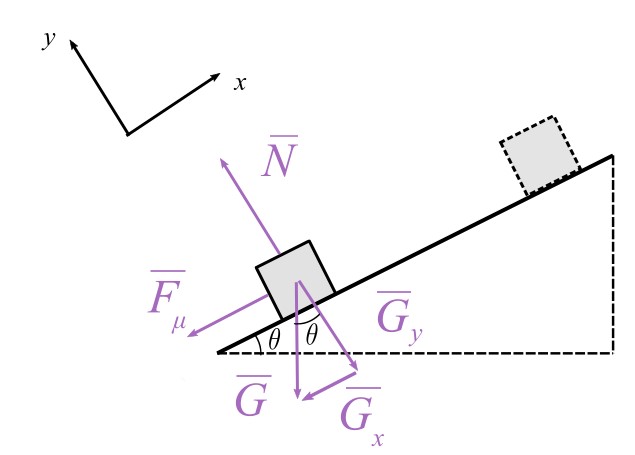
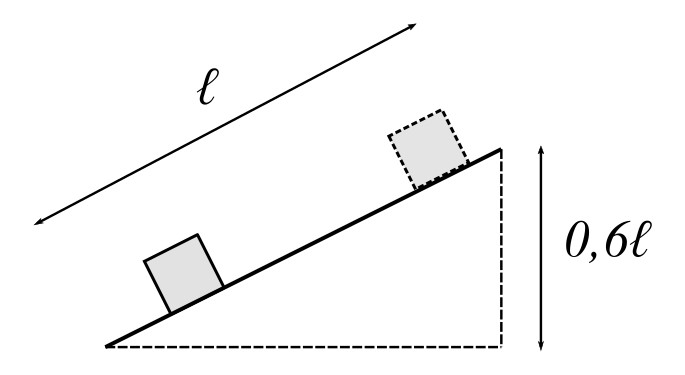
Laatikko, jolla on massa \(m\) asetetaan \(\ell\) pituiselle rampille ja sysätään liikkeelle alkunopeudella \(v_0\). Laatikko kulkee ylöspäin mentäessä ajan \(t_1\). Pysähdyttyään laatikko liukuu takaisin, jolloin aikaa on kuluu \(t_2\) verran kunnes se palaa alkuasemaansa. Lisäksi taso on asetettu sellaiseen kulmaan, että sen pystysuora korkeus \(h=0{,}6\ell\). Laske aikasuhde \(\frac{t_2}{t_1}\), kun tason ja laatikon välinen liikekitkakerroin \(\mu_k = 0{,}5\).
Tehtävässä saattaa auttaa trigonometriset identiteetit:
\(\cos \left(\sin^{-1} \left(x\right)\right)=\sqrt{1-x^2}\)
\(\sin{(\sin^{-1}{(x)})} = x\)
Tehtävä on ratkaistavissa ilman trigonometrista taulukkoa, mutta halutessaan sitä voi hyödyntää.
Ratkaisu 3.1
Rekan jarrut pettävät kesken ajon. Kuusi tonnia painavan rekan pysäyttämiseksi tielle lastataan \(60\,\mathrm{kg}\) painavia hiekkasäkkejä, joihin rekka voi törmätä. Kuinka monta hiekkasäkkiä tarvitaan, jotta saadaan hidastettua rekkaa \(75\%\) sen alkunopeudesta \(v_0 = 50\,\mathrm{\frac{km}{h}}\)? Voidaan olettaa, että törmäykset ovat täysin kimmoisia. Oletetaan myös, että törmätessä rekkaan hiekkasäkit liukuvat kitkatta maata pitkin.
Ratkaisu 3.2
Kuinka monta pingviiniä voi seistä ohuen sylinterin muotoisen jäälautan päällä, ennen kuin lautta uppoaa täysin meriveteen? Sylinterin pohjan halkaisija on \(D=15\, \mathrm{m}\) ja korkeus \(h = 1\,\mathrm{m}\). Yksi pingviini painaa \(m=30\,\mathrm{kg}\) verran.
Jään tiheys on noin \(917\, \mathrm{\frac{kg}{m^3}}\) ja meriveden \(1030\, \mathrm{\frac{kg}{m^3}}\).
Ratkaisu 3.3
Kun käsivarsi on ojennettu vaakasuoraksi sen painoa kannattelee hartialihas kuvan mukaisesti:
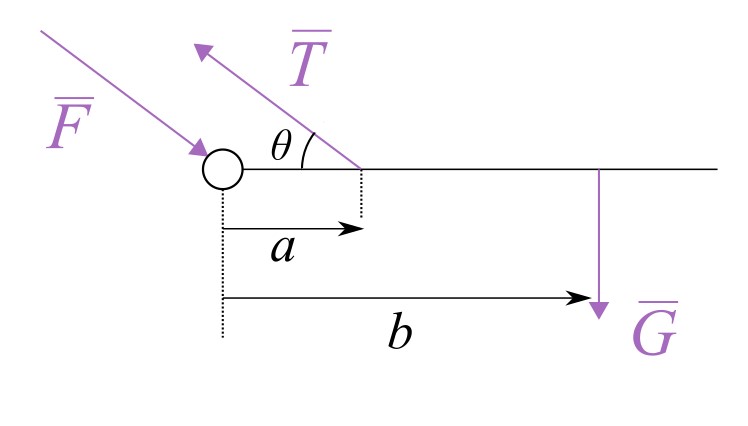
Jossa \(a = 15\,\mathrm{cm}\) ja etäisyys käsivarren massakeskipisteeseen \(b = 33\,\mathrm{cm}\). Käsivarren massa on noin \(18\,\mathrm{kg}\).
a) Ratkaise kannattelevien voimien \(T\) ja \(F\) suuruudet, kun kuvan kulma \(\theta = 17^\circ\). Voimat ovat erisuuressa kulmassa. Anna ratkaisu kolmen merkitsevän numeron tarkkuudella.
b) Kuinka suuressa kulmassa vaakasuorasta ylöspäin mitattuna voima \(F\) kohdistuu?
\begin{equation*}
\begin{array}{|r|r|}
\hline
\sqrt{1{,}23} & 1{,}10 \\ \hline
\sqrt{1{,}56} & 1{,}24 \\ \hline
\sqrt{1{,}66} & 1{,}28 \\ \hline
\sqrt{1{,}85} & 1{,}36 \\ \hline
\sqrt{1{,}92} & 1{,}38 \\ \hline
\sqrt{2{,}00} & 1{,}41 \\ \hline
\sqrt{2{,}45} & 1{,}56 \\ \hline
\sqrt{2{,}74} & 1{,}65 \\ \hline
\end{array}
\end{equation*}
Ratkaisu 3.4