5. Ääni
Tärkeimpiä asioita ovat äänen intensiteetti, intensiteettitasoja äänen kulku- ja interferenssi. Tehtävissä saa käyttää valitsemaasi kaavakokoelmaa (esim. MAOL) ja trigonometrista taulukkoa.
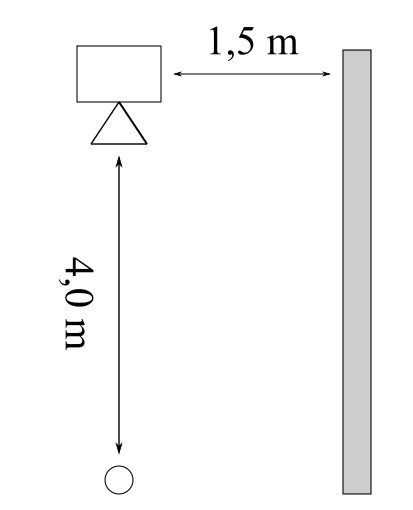
a) Kaiutin lähettää \(100\,\mathrm{dB}\) lujuudella ääntä ympärilleen. Kuinka suuri on äänen intensiteetti pisteessä, joka sijaitsee neljän metrin etäisyydellä kaiuttimesta?
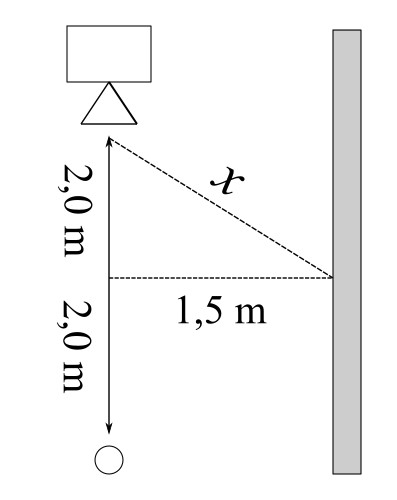
b) Tilanteeseen lisätään nyt kuvan mukaisesti seinä, joka sijaitsee \(1{,}5\,\mathrm{m}\) etäisyydellä kaiuttimesta sekä pisteestä:
Kuinka suuri on seinästä heijastuneen äänen intensiteetti pisteessä, kun seinä absorboi \(70\%\) siihen tulleesta äänestä?
Oheisen taulukon arvoista saattaa olla hyötyä:
\begin{equation*}
\begin{array}{|r|r|}
\hline
\sqrt{2} & 1{,}41 \\ \hline
\sqrt{2{,}25} & 1{,}50 \\ \hline
\sqrt{4{,}30} & 2{,}07 \\ \hline
\sqrt{5{,}75} & 2{,}39 \\ \hline
\sqrt{6{,}25} & 2{,}50 \\ \hline
\sqrt{7{,}55} & 2{,}74 \\ \hline
\end{array}
\end{equation*}
Ratkaisu 5.1
Fyysikko tiputtaa \(515 \,\mathrm{Hz}\) taajuudella värähtelevän ääniraudan kerrostalon katolta. Kuinka pitkän matkan äänirauta on pudonnut, kun fyysikon havaitsema taajuus on \(485\,\mathrm{Hz}\)?
Ratkaisu 5.2
Potilaan sisällä olevaa kasvainta tutkitaan ultraäänen avulla. Ultraäänianturi asetetaan potilaan iholle siten, että ilmaa\(^1\) ei jää anturin ja ihon väliin. Ultraäänianturi laitetaan päälle, jolloin se alkaa tuottamaan ääniaaltoja potilaaseen, joilla on \(5{,}0\,\mathrm{MHz}\) suuruinen taajuus. Ääniaaltojen aallonpituus on noin \(308 \,\mathrm{\mu m}\).
a) Anturi lähettää pulssin, jonka ensimmäinen kaiku havaitaan \(9,5\cdot10^{-6}\) sekunnin kuluttua. Kuinka syvällä kasvain on?
b) Toinen kaiku havaitaan \(4{,}84\cdot10^{-5}\) sekunnin kuluttua. Kuinka paksu kasvain on?
Huom\(^1\) -oikeassa tilanteessa ilman ja anturin väliin levitetään ultraäänigeeliä. Tällä estetään se, että ultraäänipulssit eivät vaimenisi ilmassa liikaa.
Ratkaisu 5.3