7. Sähköoppi
Tärkeimpiä asioita ovat Kirchoffin lait, Ohmin laki, sähköinen voima, sähkökentät ja kondensaattorit. Tehtävissä saa käyttää valitsemaasi kaavakokoelmaa (esim. MAOL) ja trigonometrista taulukkoa.
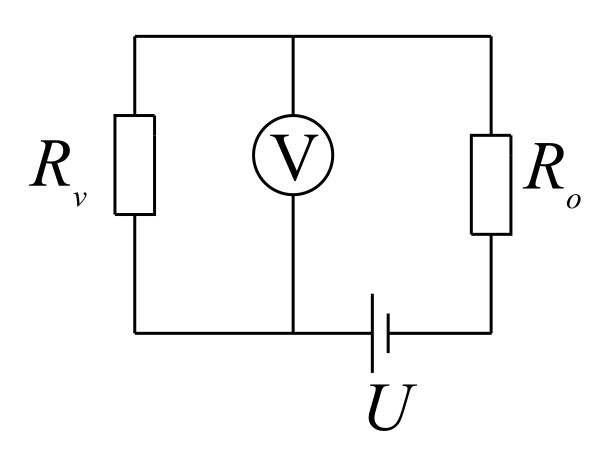
Laske oheisen kytkennän vasemman vastuksen resistanssin suuruus \(R_v\). Oikean puoleisen vastuksen suuruus \(R_o = 7{,}5\,\mathrm{V}\). Piirin keskellä on jännitemittari \(V\), jolla on sisäinen resistanssi on \(8{,}5\,\mathrm{\Omega}\). Jännitemittarin lukema on \(4{,}0\,\mathrm{V}\). Jännitelähteellä \(U=15\) V ei ole sisäistä resistanssia.
Tutkitaan kahta ilmatäytteista kondensaattoria \(A\) ja \(B\). Kondensaattori \(A\) muodostuu kahdesta \(R\)-säteisestä ympyrän muotoisesta levysta, jotka ovat etäisyydellä \(d\) toisistaan. Kondensaattori \(B\) muodostuu kahdesta neliön muotoisesta levystä, joiden sivunpituus on \(R\). Neliönmuotoiset levyt ovat etäisyydellä \(2d\) toisistaan.
a) Jos kondensaattorin \(A\) kapasitanssi on \(C_A\), osoita että kondensaattorin \(B\) kapasitanssi \(C_B = \frac{C_A}{2\pi}\).
b) Kondensaattori \(A\) levyjen välinen matka täytetään nyt tuntemattomalla eristeellä. Mikä tulee olla eristeen suhteellinen permittiivistyys, jotta kondensaattorin \(B\) kapasitanssi on yhtä suuri kuin kondensaattori \(A\) kapasitanssi?
Ratkaisu 7.2
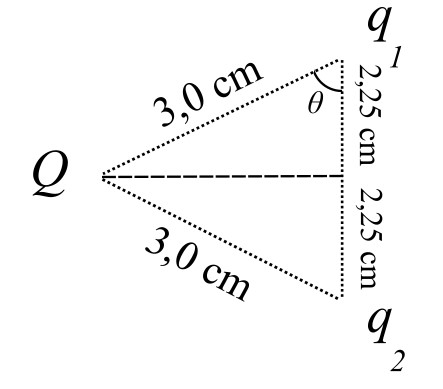
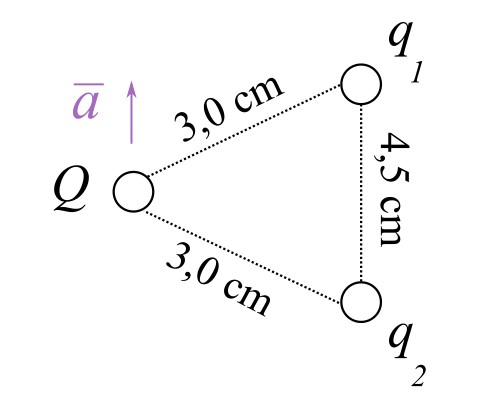
Tutkitaan kuvan mukaista systeemiä, joka koostuu pistevarauksista \(q_1\) ja \(q_2\) jotka sijaitsevat etäisyydellä \(4,5\,\mathrm{cm}\) toisistaan. Pistevaraukset ovat kiinnitetty paikalleen, jolloin ne eivät voi liikkua. Systeemiin tuodaan pistevaraus, jonka varauksen suuruus \(Q =-2{,}0\,\mathrm{nC}\) ja massa \(m = 5{,}5\,\mathrm{g}\). Varausten \(q_1\) ja \(q_2\) takia varaus \(Q\) lähtee kiihtyvyydellä \(a = 305\,\mathrm{\frac{m}{s^2}}\) suoraan ylöspäin heti kun se vapautetaan. Ratkaiste varausten \(q_1\) ja \(q_2\) suuruus yksikössä \(\mathrm{nC}\).
Kondensaattori, jonka kapasitanssi on \(6{,}0\,\mathrm{\mu F}\) on alkutilanteessa varaukseton. Kondensaattori on kytketty rinnan vastuksen \(5{,}0\,\mathrm{\Omega}\) ja ideaalisen jännitelähteen \(50{,}0\,\mathrm{V}\). Kuinka suuri on kondensaattorin varaus, kun vastus kuluttaa tehoa \(250\,\mathrm{W}\) verran?
Ratkaisu 7.4
Auton akun lähdejännite on \(13{,}2\,\mathrm{V}\) suuruinen. Oletetaan, että akulla ei ole sisäistä resistanssia. Akkuun on sarjaan kytkettynä \(R=3{,}5\,\mathrm{\Omega}\) suuruinen vastus sekä termistori\(^1\). Termistorin jännite ei noudata Ohmin lakia, vaan sen jännite noudattaa toisen asteen yhtälöä \(U = aI+bI^2\), jossa vakiot \(a = 4{,}0\,\mathrm{\frac{\Omega}{A}}\) ja \(b = 1{,}4\,\mathrm{\frac{\Omega}{A}}\). Kuinka suuri virta kulkee vastuksen \(R\) läpi?
\begin{equation*}
\begin{array}{|r|r|}
\hline
\sqrt{2} & 1{,}41 \\ \hline
\sqrt{10} & 3{,}16 \\ \hline
\sqrt{11} & 3{,}31 \\ \hline
\sqrt{12} & 3{,}46 \\ \hline
\sqrt{13} & 3{,}60 \\ \hline
\sqrt{14} & 3{,}74 \\ \hline
\end{array}
\end{equation*}
Termistori\(^1\) on vastus, jonka resistanssi riippuu lämpötilasta.
Ratkaisu 7.5